La teoria dei grafi spiegata ai bambini

bussolascuola dicembre 27, 2023 matematica,

La teoria dei grafi spiegata ai bambini

In matematica, informatica e, più in particolare, geometria combinatoria, la teoria dei grafi studia appunto i grafi, cioè strutture matematiche costituite da nodi o vertici e archi che li collegano, utilizzate in topologia, teoria degli automi, funzioni speciali, geometria dei poliedri, algebre di Lie, ma anche in informatica per schematizzare programmi, circuiti, reti di computer, mappe di siti.

I grafi sono alla base di modelli e processi studiati nell'ingegneria, nella chimica, nella biologia molecolare, nella ricerca operativa, nella organizzazione aziendale, nella geografia (sistemi fluviali, reti stradali, trasporti), nella linguistica , nella storia (alberi genealogici e filologia dei testi), e possono modellare molti problemi del mondo in cui viviamo.

La teoria dei grafi è diventata un ambito della matematica ricco di applicazioni nell'ambito della combinatoria e del calcolo automatico.

I grafi sono oggetti matematicamente ricchi che si prestano facilmente ad un approccio precoce in ambito educativo. Ovviamente con le opportune strategie didattiche adatte all'età degli studenti.

Di seguito percorsi, esempi e materiali adatti ad attività con gli alunni di scuola primaria

Una prima lezione alla teoria dei grafi.
Prendere familiarità con la teoria dei grafi. Viene spiegato ciò che i rappresentanti delle scienze esatte chiamano grafici, introdotti i concetti principali e i nomi degli elementi del grafico. Analizzati esempi e compiti. Viene mostrato agli studenti l'uso pratico della teoria dei grafi, utilizzando esempi storici, moderni e quotidiani.

Infine una serie di video, accompagnati da attività, consentono di apprendere meglio e consolidare le nuove conoscenze.

Viene spiegato ciò che le scienze esatte chiamano grafici, introducendo i concetti di base e i nomi degli elementi di un grafico. Si analizzano esempi e compiti. Durante la lezione, si cerca di mostrare agli studenti l'applicazione pratica della teoria dei grafi, utilizzando esempi storici e moderni che ci circondano ogni giorno. Al fine di apprendere meglio e consolidare nuove conoscenze, oltre al video, vengono presentate delle attività.

Da seguire con i sottotitoli in italiano

Per chi ha svolto la prima lezione.

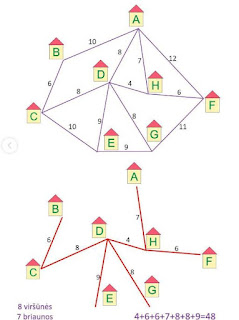
Durante la lezione vengono introdotti i grafici ponderati, completi ed esempi di tipo ad albero.

Vengono presentate le formule per calcolare i bordi dei grafici e l'algoritmo di Kruskal.

Dopo la lezione, è consigliato fare il test proposto con Kahoot

Qui i materiali delle lezioni (utilizzare con traduttore) https://www.septintasfortas.lt/matematika-pamokos/ video da utilizzare con sottotitoli

Qui due percorsi a cura di Joel David Hamkins, professore di matematica, filosofia e computer science presso la City University of New York, che ha voluto esplorare alcune idee elementari in teoria dei grafi con le bambine di una classe terza elementare, frequentata dalla figlia.