Numeri in classe prima: idee utili da neuroscienze, psicologia cognitiva e didattica

Numeri in classe prima: strategie coinvolgenti e scientificamente fondate

A cura di Sonia Gabrielli, insegnante di scuola primaria

Introduzione

L’apprendimento dei numeri in classe prima è un momento cruciale: qui si costruiscono le basi non solo per il calcolo, ma per la comprensione profonda della matematica. Le ricerche neuroscientifiche degli ultimi anni – tra cui quelle condotte da Daniela Lucangeli (Università di Padova) – ci confermano che il percorso verso la competenza numerica è più efficace quando integra esperienze concrete, stimolazione multisensoriale e una dimensione emotiva positiva.

In questo articolo esploriamo strategie pratiche per lavorare con i numeri in classe prima, spiegando perché funzionano e fornendo esempi concreti da usare in classe.

Perché partire dal “senso del numero”

Il cervello dei bambini e i numeri

Secondo Lucangeli, l’idea di numero nasce dall’esperienza: il bambino costruisce il concetto numerico attraverso il corpo, lo spazio e il tempo.

• L’area intraparietale del cervello elabora la quantità e la posizione nello spazio, formando una linea mentale dei numeri.
• L’associazione tra movimento, immagine visiva e linguaggio rafforza il ricordo e il recupero delle informazioni.
• Le emozioni positive attivano sistemi neurochimici (dopamina, ossitocina) che migliorano motivazione e consolidamento della memoria.

Per approfondire

UNICOG - Cognitive Neuroimaging
Labsiegler.tc.columbia.edu

La prof.ssa Daniela Lucangeli, ordinaria di Psicologia dell’educazione e dello sviluppo all’Università di Padova, ha approfondito il concetto di “intelligenza numerica” come meccanismo innato, che necessita di essere nutrito fin dai primi anni della vita. In un’intervista afferma:

«Non bisogna aspettare la scuola per nutrire l’intelligenza di quantità… i primi cinque anni sono determinanti»
e avverte che una didattica basata prevalentemente sul calcolo scritto «rischia di determinare questa “cecità al numero”», laddove la manipolazione concreta sarebbe fondamentale.

 

direfareinsegnare.education

Nel suo lavoro (con Poli e Molin), L’intelligenza numerica. Abilità cognitive e metacognitive nella costruzione della conoscenza numerica, presenta strumenti didattici, analogici e simbolici, per sviluppare la conoscenza numerica nei bambini di età prescolare e primaria, prevenendo difficoltà di apprendimento. Erickson

In campo clinico e psicoeducativo, Lucangeli ha contribuito ad elaborare test e interventi calibrati sulla metacognizione e le basi cognitive della cognizione numerica, con particolare attenzione a difficoltà come la discalculia. Università di Padova - RicercaWikipedia

Perché (ancora) partire dall’esperienza

Le neuroscienze e la psicologia dello sviluppo convergono su un punto: il senso del numero si costruisce quando i bambini collegano quantità, azioni ed esperienze corporee a rappresentazioni sempre più astratte. La ricerca mostra che la qualità delle esperienze informali con i numeri (giochi, linee dei numeri, conversazioni) predice parte delle differenze iniziali in matematica e che interventi mirati possono ridurre i divari. 

>> gablab.mit.eduTaylor & Francis

Intelligenza numerica precoce: Lucangeli ci ricorda che il bambino possiede un’intelligenza di quantità già nei primi cinque anni: capacità di riconoscere quantità, confrontare “di più/di meno”, usare le dita per contare fanno parte del suo patrimonio cognitivo innato. Questo va valorizzato prima ancora che arrivi la scuola, pena “cecità al numero” e apprendimento meccanico. >> direfareinsegnare.education

Potenziare attraverso la manipolazione: Il suo approccio valorizza le attività analogiche e visuo-spaziali (come quelle presenti nel suo volume sopra citato), che permettono di passare dalle quantità percettive ai simboli. >> Erickson

Attività

Manipolazione precoce e giochi analogici

Attività con oggetti, dita, linee, e simboli, pensate per “nutrire l’intelligenza numerica” attraverso esperienze dirette e concrete. Tutto questo è coerente con il suo invito a non attendere la scuola per stimolare queste abilità. 

>> direfareinsegnare.education

Kit e strumenti ufficiali

L’intelligenza numerica 1 (Lucangeli, Poli, Molin) propone giochi e software che stimolano processi semantici, lessicali, sintattici e la conoscenza del counting in età prescolare e primaria. 

>> Erickson

Attenzione ai segnali precoci e prevenzione

Lucangeli partecipa a numerosi progetti che sviluppano strumenti per la valutazione e l'intervento precoce (screening, training metacognitivo e visuo-spaziale), fondamentale nella prevenzione di falsi positivi nella diagnosi di discalculia e difficoltà matematiche.
>> Università di Padova - RicercaWikipedia

Cinque principi operativi (con basi solide)

1. Rappresentazioni multiple e “concreteness fading”
   Avvia con oggetti reali e immagini, poi fai emergere strutture sempre più astratte (punti → rekenrek → linea dei numeri → cifre ed espressioni), esplicitando ogni ponte tra una rappresentazione e l’altra. Questo percorso “dal concreto all’astratto” migliora la comprensione e il trasferimento a problemi nuovi, purché le connessioni siano rese esplicite >> ResearchGatePMC

2. Pratica distribuita (spacing)
   Meglio poco e spesso che tanto tutto insieme: distanziare nel tempo le esperienze rende l’apprendimento più stabile nei bambini della primaria. Programma micro-ripassi di 5–7 minuti più volte a settimana. >> PMCaugmentingcognition.com

3. Recupero attivo (retrieval practice)
   Non solo spiegare: chiedi ai bambini di ricordare e ricostruire (senza guardare), con domande, giochi “io dico/tu mostri”, mini-quiz orali e con oggetti. Il recupero attivo consolida più della sola rilettura o ripetizione passiva. >> PubMedBruce Hayes

4. Interleaving (alternanza ragionata)
   Mescola mini-attività su idee vicine (quantità ↔ ordine ↔ decomposizioni) per aiutare a discriminare somiglianze e differenze; evita lunghi blocchi monotematici. >> SpringerLink

5. Gioco strutturato con linea dei numeri
   Giochi da tavolo lineari (caselle in fila 1→10→20) potenziano il senso di grandezza, il conteggio e l’identificazione di numeri, con effetti che si mantengono nel tempo. Evita piste circolari nelle fasi iniziali. >> Carnegie Mellon UniversityERIC

Inoltre corpo e spazio: camminare, saltare, spostare oggetti dà un ancoraggio percettivo alle quantità e alla linea dei numeri. >> Taylor & Francis

Routine e attività per la classe prima

1) Subitizing & strutture visive (3–6 minuti, quotidiano)

• Flash di dot-patterns (configurazioni del dado/domino, 1–6): mostra per 1–2 secondi, copri e chiedi “Quanti? Come li hai visti?”.
• Variazioni: stessi totali con strutture diverse (es. 5 come 2+3, poi 4+1) e confronto veloce “più/meno/uguale”.
• Perché funziona: allena l’attenzione alle partizioni e prepara alle strategie di calcolo entro la decina. >> ResearchGate

2) Rekenrek e decomposizioni

• Sequenze: mostra 5 (tutta la fila rossa), poi “5 e 1”, “5 e 2”, … fino a 10; verbalizza sempre la struttura (“Lo vedo come 5 e 2”).
• Passaggio alla linea dei numeri: “Dove abita 7? È 5 e 2… allora sta due passi dopo il 5”.
• Legame con la ricerca: mappare grandezze su strutture lineari sostiene lo sviluppo di strategie e stime più accurate. >> siegler.tc.columbia.edu

3) Giochi lineari dei numeri (10–15 minuti)

• Pista 1–20: un dado 1–3; ogni mossa richiede di dire da a (“Ero sul 6, faccio 2 passi: 7, 8”).
• Carte “salti intelligenti”: +2, +3, −1 per introdurre differenze e inversi.
• Effetti attesi: migliorano conteggio, riconoscimento di numerali e comprensione di grandezza. >> Carnegie Mellon University

4) Ginnastica delle dita (finger gnosis) (3 minuti)

• Ad occhi chiusi: tocca un dito della mano del bambino (o due insieme); lui nomina quale/i.
• “Mostra X con le dita in due modi diversi” (es. 4 = 1+3, 2+2).
• Perché è utile: la consapevolezza digitale è legata all’avvio delle abilità numeriche; interventi brevi di training mostrano effetti su compiti aritmetici in prima. >> PMCjnc.psychopen.euFrontiers

5) Number Talks & conta corale (5–10 minuti)

• Domande essenziali: “Quanti modi per fare 8?”, “Come lo sai?”, “Qual è la tua prima mossa per arrivare a 10?”.
• Conta corale avanti/indietro con fermate strategiche (pausa su 9→10 per evidenziare il cambio di decina).
• Perché funziona: recupero attivo, verbalizzazione delle strategie e confronto tra rappresentazioni. >> Bruce Hayes

>> Number Talks

6) Problemi in contesti “snelli”

Storie minime con numeri piccoli e oggetti reali (tappi, bastoncini, carte puntinate). Evita un eccesso di dettagli tematici nelle prime fasi, che può vincolare il trasferimento. Mantieni generica la struttura mentre sfumi il supporto concreto. >> PM

    

Modelli di attività pronte per l’aula

Il tavolo della quantità
Creare un’area in classe con materiali di vario tipo (pietre, conchiglie, mattoncini, tappi) da usare per giochi di raggruppamento, confronto, seriazione.
Obiettivo: rafforzare il senso del numero e la stima di quantità.

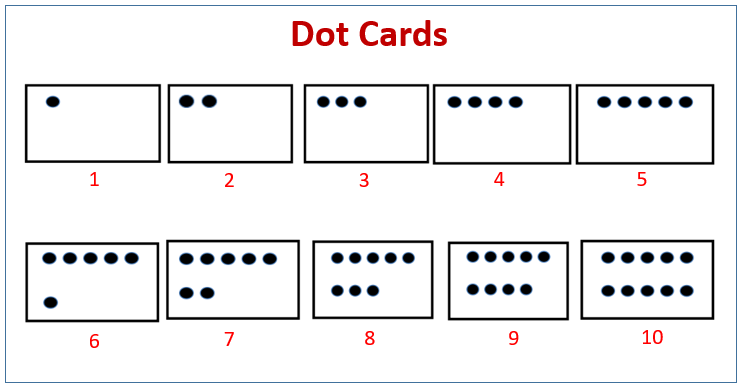
Subitizing visivo (flash di 2–3 secondi)

Giochi di corrispondenza e subitizing
Proporre carte o schede con rappresentazioni diverse della stessa quantità (punti, dita, oggetti) per allenare il riconoscimento rapido senza contare.

Obiettivo: riconoscere quantità senza contare, vedere strutture (5 e 10).
Come: mostrare dot cards per 2–3 s; chiedere “Cosa hai visto? Come lo sai?”. Varianti: stessi totali con configurazioni diverse; comporre/scomporre (5 come 2+3).
Perché funziona: potenzia stime di quantità e strategie additive precoci. Materiali pronti all’uso nelle “dot cards” (immagine sopra).

Rekenrek routine (1–2 minuti al giorno)

Rekenrek – Strumento a perline colorate organizzate in file da 5 o 10, utile per visualizzare quantità, composizioni come 5 + 3 e supportare il calcolo attraverso la subitizing.

Obiettivo: interiorizzare strutture di 5 e 10, automatizzare fatti entro il 20.
Come: mostrare configurazioni, chiedere spiegazioni (“vedo 5 rossi e 3 bianchi: 8”). Collegare subito a espressioni (8=5+3).
Perché funziona: modello lineare-strutturale che riduce il carico cognitivo rispetto al conteggio unitario; supportato da evidenze su apprendimenti precoci e traiettorie. (Vedi immagini rekenrek sopra.) >> Taylor & Francis

Linea dei numeri a grandezza naturale

Linee dei numeri giganti
Usare nastri adesivi sul pavimento per creare linee numeriche percorribili a piedi, favorendo l’associazione tra numero e posizione nello spazio.

Obiettivo: mappare quantità → spazio → numero, stimare posizioni, capire “più/meno” come distanza.
Come: nastro sul pavimento, tacche equidistanti 0–20; attività motorie (salto di +2, –1; “Dove sta l’8 tra 0 e 10?”).
Perché funziona: rappresentazioni lineari ben calibrate predicono migliore stima numerica e supportano calcolo mentale. (Vedi immagini sopra.) 

>> PubMed

Giochi da tavolo lineari 1–20

Obiettivo: raffinare la rappresentazione lineare delle grandezze e il conteggio in avanti/indietro.
Come: percorsi rettilinei numerati; si avanza di tanti passi quanti indica il dado, dicendo i numeri delle caselle.
Perché funziona: i board games lineari aumentano confronto di grandezze, stima sulla linea e facilitano futuri apprendimenti aritmetici, più dei giochi a percorso circolare o non numerati. 

Descrizione: tabellone con caselle numerate in sequenza, pedine e carte con istruzioni (+1, −2, “salta al 10”, “vai due passi prima del 7”).

Come funziona: i bambini spostano la pedina in base alla carta pescata, contano ad alta voce, osservano la posizione.

Perché funziona:

• Rafforza la mental number line (Lucangeli, 2017).
• Integra linguaggio e visione spaziale.
• Introduce la nozione di operazione come spostamento.

Come utilizzare questi giochi in classe

Elemento	Vantaggio pedagogico
Percorso lineare (1–20)	Rende intuitiva la nozione di ordine, succedersi e distanza tra i numeri.
Attività motoria + verbale	Il movimento della pedina e la lettura ad alta voce consolidano il senso di numero come posizione.
Rappresentational mapping	Collegamento chiaro tra la rappresentazione fisica (percorso) e la linea dei numeri mentale, migliorando l’aritmetica (Siegler & Ramani, 2009) ScienceDirect.

Indicazioni operative per l’uso in aula

Materiali necessari:

Stampa o crea un grande tabellone lineare 1–20.
Pedine e dado (preferibilmente 1–3) per movimentare il gioco.

Modalità di gioco:

A turno, ogni bambino tira il dado e sposta la propria pedina.
Deve dire ad alta voce i numeri attraversati (“Sono sul 5, ora il 6, poi il 7…”), per favorire il conteggio verbale e associativo.

Varianti didattiche:

Schede domande: “Qual è 2 passi dopo il 8?”, “Se sei sul 14 e fai −3, dove arrivi?”
Aggiungi carte “+2” o “−1” per integrare operazioni semplici.

Confronta questa versione lineare con una versione circolare: discuterne insieme rinforza la comprensione della linearità numerica.

Counting Collections (collezioni da contare)

Obiettivo: passare dal conteggio per 1 al raggruppamento in 2, 5, 10; introdurre base dieci senza schede.
Come: sacchetti con bottoni/paste/clip; i bambini decidono come organizzare e tenere traccia; documentano con disegni/equazioni.
Perché funziona: crea connessioni tra strategia, rappresentazione e linguaggio matematico; si innesta sulle learning trajectories note (conteggio → raggruppamento → valore posizionale). 

>> Taylor & Francis

“Parla-pensa-mostra” (number talks brevi)

Obiettivo: emersione di strategie, metacognizione, lessico matematico.
Come: problemi orali molto semplici (es. 9+3, 14–9), tempo di pensiero, condivisione di strategie diverse ancorate a rekenrek/linea/dieci-frame.
Perché funziona: integra recupero attivo e spiegazione, due leve con solide basi sperimentali. >> learningtrajectories.org

Mani e dita come strumenti cognitivi

Obiettivo: coordinazione quantità-gesto, mappatura parte/tutto.
Come: giochi di finger-gnosia (toccare dita senza guardare, imitare pattern, “mostra 7 in due modi”); collegare a rekenrek e a fatti di 10.
Nota di prudenza: alcuni studi mostrano associazioni e possibili effetti di training, ma l’evidenza è eterogenea; usiamole come ponte, non come fine. 

>> ResearchGate

Micro-sessioni di pratica “spaziata & mista”

Obiettivo: consolidare senza noia.
Come: 5 minuti al giorno con 5–6 prompt misti (subitizing, stima sulla linea, un fatto entro 10, un confronto > <, un “spiega come sai”). Ripassare gli stessi obiettivi a distanza di giorni.
Perché funziona: distribuzione e variazione potenziano ritenzione e trasferimento. >> learningtrajectories.org

Software e strumenti strutturati
Utilizzare attività interattive come per esempio il kit L’intelligenza numerica di Lucangeli, Poli e Molin, che lavora su processi semantici, lessicali e sintattici del numero attraverso il gioco.

Una micro-progressione per le prime 6 settimane

Settimane 1–2

Subitizing quotidiano 1–5; rekenrek fino a 5; linea dei numeri 0–10 (saltelli di +1/−1).
Giochi: pista 1–10 con dado 1–2.

Valutazione iniziale informale: riconoscimento cifre 0–10, corrispondenza quantità↔cifra.

Settimane 3–4

Subitizing 1–6 (configurazioni variate).
Rekenrek fino a 10; decomposizioni di 6–10; primi ponti al simbolico (6 = 4+2 ecc.).
Pista 1–20, carte +2/−1; prime storie di addizione/rimozione.

Recupero attivo: mini-quiz orali “Senza guardare: fai 7 con le dita in due modi”.

Settimane 5–6

Linea dei numeri 0–20 con “fermate” alla decina; salti di +2/+3.
Equivalenze strutturali: 8 come 5+3 ↔ posizione sulla linea ↔ pattern di punti.
Didattica a stazioni: alterna 6 brevi stazioni (subitizing, rekenrek, linea, problemi, giochi lineari, registro simbolico).

Questa progressione realizza concreteness fading (oggetti → schemi → simboli) con spacing, retrieval e interleaving incorporati. ResearchGateaugmentingcognition.comPubMedSpringerLink

Valutazione formativa (rapida ma informativa) “leggera” (che fa apprendere)

• Stime sulla linea: “Dov’è il 7 tra 0 e 10? E il 14 tra 0 e 20?” (guardare la coerenza più dell’esattezza puntuale). >> PubMed
• Racconta la tua strategia: rubric a 3 livelli (conta-tutto → raggruppa/compone → usa relazioni 5/10). >> Taylor & Francis
• Spaced checks: 4–6 item misti, senza tempo, ogni 5–7 giorni; riprendere ciò che non è stabile. >> learningtrajectories.org
• Exit ticket orale (30 secondi): “Mostrami 7 sul rekenrek in due modi”.
• Mini-sondaggi a tappeto: dita sotto il banco → al segnale “mostra 6”, poi chiedi “Chi l’ha fatto 5+1? Chi 3+3?”.
• Diari visivi: ogni bambino fotografa (o disegna) un modo diverso di vedere 8; la settimana dopo prova a ricordarli senza guardare (retrieval). Bruce Hay

Inclusione e bisogni educativi speciali

riconoscere precocemente segnali di rischio per discalculia

• Attenzione a campanelli ricorrenti nonostante l’insegnamento: difficoltà marcate e persistenti nel collegare quantità e cifre, nell’ordinare numeri, nel subitizing del dado/domino, nel ricordare fatti aritmetici molto semplici, nell’orientarsi su una linea dei numeri. In questi casi:
• Osservare sistematicamente con compiti brevi su confronto di quantità, enumerazione, localizzazione su linea dei numeri.
• Confrontarsi con il team e la famiglia; valutare l’uso di screening standardizzati come primo passo informativo (es. strumenti ispirati al Dyscalculia Screener di Butterworth; l’eventuale diagnosi richiede test psicometrici e criteri clinici). Digital Commons USFPMC
• In classe, risulta utile didattica esplicita, multisensoriale e progressiva, con collegamenti ripetuti quantità↔parola↔cifra↔posizione. dyslexiafoundation.org
• Diagnosi precoce delle difficoltà numeriche: strumenti di screening (es. Dyscalculia Screener) esistono dai 6 anni in su; in prima primaria è fondamentale la prevenzione con esperienze ricche e guidate. >> EEF
• Strumenti di screening per la discalculia sviluppati da Lucangeli e collaboratori sono principalmente il Test di Discalculia Informatizzato (Lucangeli, Tressoldi, Molin, Poli, & Zorzi) e il ABCA (Valutazione del Calcolo Aritmetico). Il primo è un test informatizzato che valuta le abilità di calcolo dalla terza elementare alla terza media, analizzando quattro aree specifiche: senso del numero, fatti numerici, dettato di numeri e calcolo a mente, Erickson. L'ABCA, invece, è uno strumento cartaceo che si concentra sulla valutazione del calcolo aritmetico
• Accessibilità: routine prevedibili, gesti/visuali consistenti (stesse configurazioni per 5 e 10), linguaggio esplicito e multimodale. >> Taylor & Francis

Materiali poveri, impatto alto

• Tappi / sassolini in sacchetti da 10; domino; rekenrek artigianale (cartone + cannucce + perline); piste lineari stampate 1–20; carte salto (+1,+2,−1, “torna al 10”).
• Linee dei numeri fisiche sul pavimento: camminare i salti e poi “dirli senza camminare”.
• Materiali manipolativi

• Abaco a 20 palline: per contare, fare salti di 2, di 5, confrontare quantità.
• Reggi libri numerici (numeri stampati su cubi): per costruire sequenze e fare confronti.
• Linee dei numeri in classe: corda o nastro con cartoncini numerati appesi.
• Attività motorie numeriche
• Portare il corpo nel conteggio: saltare sulle caselle, camminare lungo una linea numerata disegnata a terra, lanciare un dado e fare passi corrispondenti.Motivazione neuroscientifica: movimento + conteggio = consolidamento nelle aree cerebrali visuo-spaziali e motorie.

Perché tutto questo funziona

Daniela Lucangeli evidenzia che:

1. La sequenzialità fisica riprodotta nei giochi lineari attiva la linea mentale dei numeri, fondamentale per orientarsi nel calcolo.
2. L’integrazione visivo–spaziale–linguistica rende l’informazione più stabile in memoria a lungo termine.
3. La dimensione ludica genera emozioni positive che abbassano l’ansia da prestazione e aumentano la motivazione intrinseca.
4. L’uso di operazioni come “+2” o “salta al 15” stimola il calcolo ragionato, rafforzando la flessibilità numerica.

In classe prima non “insegniamo conti”: alleniamo occhi, mani, voce e mente a vedere strutture, a muoversi sulla linea, a parlare di strategie. Con routine brevi, giochi lineari, modelli coerenti e pratica distribuita, i bambini costruiscono davvero il numero — e lo portano con sé negli anni.

Quando trasformiamo l’apprendimento numerico in un’esperienza concreta, gioiosa e multisensoriale, non stiamo solo insegnando matematica: stiamo costruendo nei bambini un rapporto positivo con il pensiero logico, che li accompagnerà per tutta la vita scolastica.

Le attività sopra descritte si basano su evidenze scientifiche che dimostrano come:

• Il passaggio dall’analogico al simbolico faciliti la comprensione (Dehaene, 2011; Lucangeli et al., 2003).
• La dimensione emotiva dell’apprendimento numerico sia determinante (Lucangeli, 2020).
• La stimolazione precoce e diversificata prevenga difficoltà persistenti (Butterworth, 2013; Lucangeli, 2004).

Riferimenti bibliografici per approfondire

Lucangeli, D., Poli, S., Molin, A. (2003). L’intelligenza numerica. Abilità cognitive e metacognitive nella costruzione della conoscenza numerica dai 6 agli 8 anni (Vol. 2). Erickson. Erickson

Lucangeli, D. (intervista). L’intelligenza di quantità come meccanismo innato da nutrire precocemente, e i rischi dell’apprendimento freddo e verbale. direfareinsegnare.education

Lucangeli, D., e collaborazione nel Dip. di Psicologia dello Sviluppo, con numerosi contributi su cognizione numerica, disturbi dell’apprendimento, screening e intervento. Università di Padova - RicercaWikipedia

Dehaene, S. (2011). The Number Sense: How the Mind Creates Mathematics (Rev. & Updated ed.). Oxford University Press. Sintesi accessibile del substrato neurocognitivo del numero. gablab.mit.edu

(panoramica su basi neurali del numero). UNICOG - Cognitive Neuroimaging Lab

Clements, D. H., & Sarama, J. (2020). Learning and Teaching Early Math: The Learning Trajectories Approach (3rd ed.). Routledge. Quadro operativo per progettare progressioni e attività. Taylor & Francis

Siegler, R. S., & Booth, J. L. (2004). Development of numerical estimation in young children. Child Development, 75(2), 428–444. Rilevanza della rappresentazione lineare delle grandezze. PubMed

Siegler, R. S., & Ramani, G. B. (2009). Playing linear number board games—but not circular ones—improves low-income preschoolers’ numerical understanding. Journal of Educational Psychology, 101(3), 545–560. Evidenze su board games lineari.  Linea dei numeri e giochi lineari (evidenza di impatto e stabilità). siegler.tc.columbia.eduCarnegie Mellon University

Siegler, R. S., & Ramani, G. B. (2008). Playing linear numerical board games promotes low-income children's numerical development. Developmental Science, 11(5), 655–661. Studio cardine sull’efficacia dei percorsi lineari.

Butterworth, B. (2003/2005). Dyscalculia Screener. nferNelson/GL Assessment. Strumento standardizzato di screening (6–14 anni). EEF

Learning Trajectories: guida sintetica online e materiali operativi. learningtrajectories.org

Roediger & Karpicke; Cepeda et al. su retrieval practice e spacing. Bruce Hayesaugmentingcognition.com
Finger gnosis e primi numeri (rassegne e interventi). PMCjnc.psychopen.eu
Clements & Sarama su learning trajectories in matematica precoce. mheducation.com
Fyfe & McNeil su concreteness fading (rassegna e studi sul trasferimento). ResearchGate