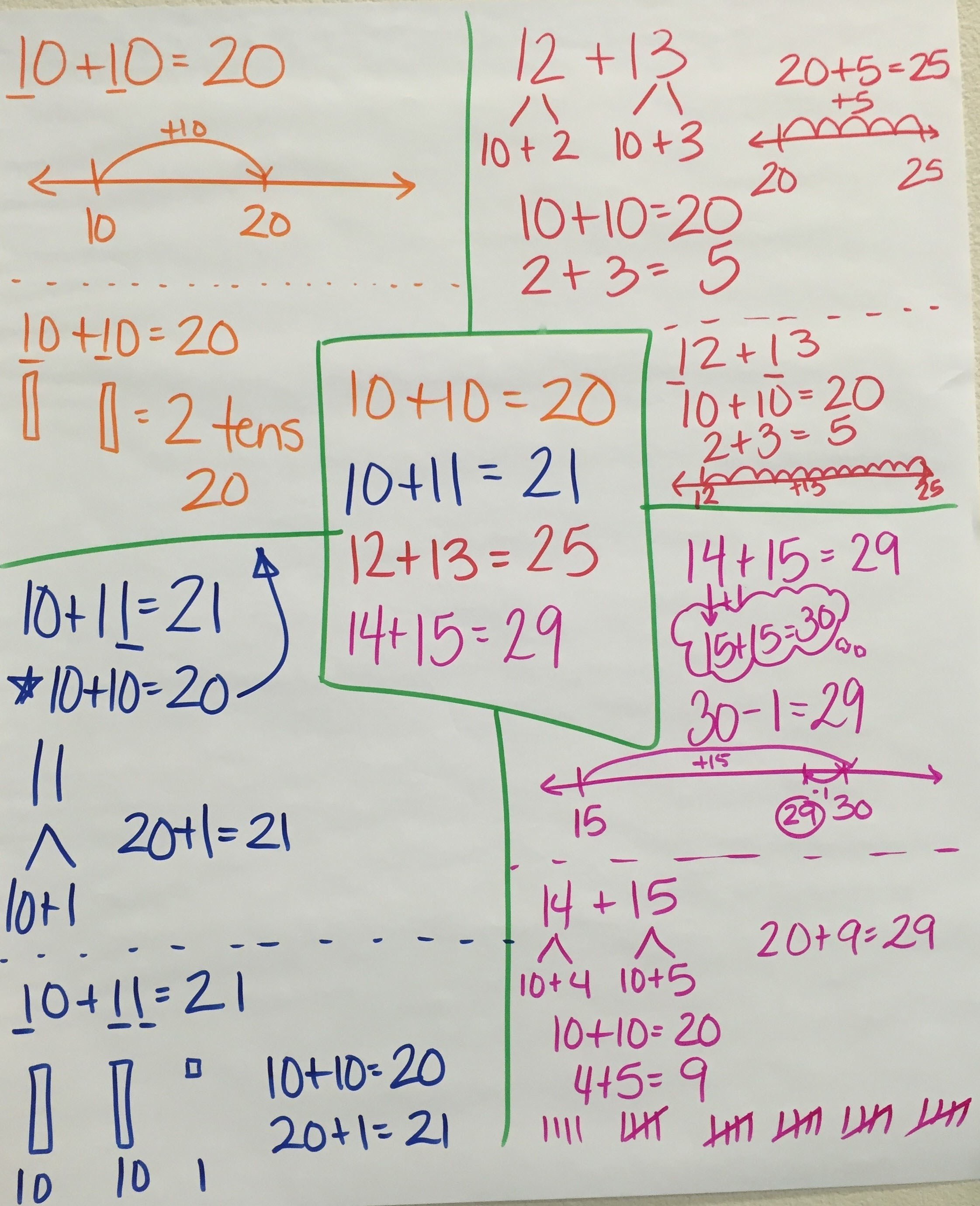
Number Talk è una routine matematica da dieci a quindici minuti in cui agli studenti viene chiesto di risolvere i problemi mentalmente. Gli studenti sono incoraggiati ad usare una varietà di strategie (contare, scomporre numeri, differenza costante, ecc.) Per risolvere un problema di matematica (frazioni, addizioni, sottrazioni, tempo, moltiplicazione, divisione, il nome).
In tutto il mondo la memorizzazione dei fatti di matematica di base è un dibattito continuo.
Quando vengono utilizzati nel tempo, i Numbers Talks aiutano gli studenti a dare un senso alla matematica, a dare priorità alle strategie e ad apprendere i fatti di base e l'apprendimento è molto più potente della memorizzazione.
Il senso del numero è la capacità di comprendere numeri e quantità, utilizzare i numeri in modo flessibile ed eseguire calcoli mentalmente.
Quando vengono utilizzati nel tempo, i Numbers Talks aiutano gli studenti a dare un senso alla matematica, a dare priorità alle strategie e ad apprendere i fatti di base e l'apprendimento è molto più potente della memorizzazione.
Il senso del numero è la capacità di comprendere numeri e quantità, utilizzare i numeri in modo flessibile ed eseguire calcoli mentalmente.
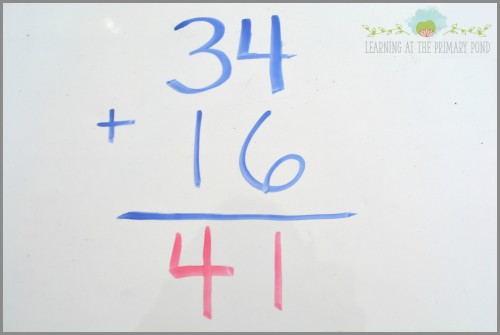 |
| https://learningattheprimarypond.com/blog/how-to-do-number-talks/ |
Se uno studente fa questo errore, vuol dire che probabilmente NON comprende VERAMENTE quale voglia significare addizionare con più cifre. Sappiamo che risolvere questo problema richiede la formazione di un gruppo di dieci (6 + 4 = 10), e quindi aggiungere quel gruppo di dieci agli altri (30 + 10), per un totale di 5 gruppi da dieci (50).
Uno studente che fa l'errore di cui sopra si basa sull'algoritmo che ha appreso (e appreso in modo errato).
Lo scopo di sviluppare il senso del numero negli studenti è che capiscano i concetti sottostanti delle operazioni che eseguono (addizione, sottrazione, moltiplicazione, divisione).
Gli studenti che hanno un forte senso del numero possono risolvere i problemi in più di un modo e verificare che le loro risposte abbiano un senso.


Gli studenti spiegano il loro modo di pensare.
Una volta annotate tutte le soluzioni, l'insegnante chiede agli studenti di spiegare come hanno ottenuto la loro soluzione. Gli studenti spiegano (dal loro posto) mentre l'insegnante scrive i passi che descrivono alla lavagna.
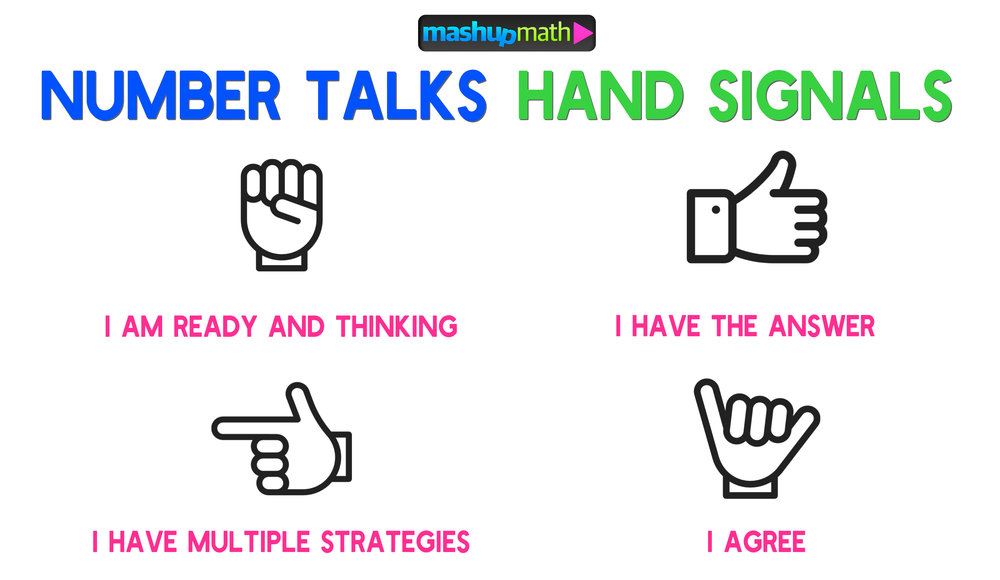 Esempio di Number Talk
Esempio di Number Talk
Insegnante:
(Scrive 9 + 17 alla lavagna). (Uno studente inizia a muovere il braccio in aria.) Quando hai la risposta, mostrami il pollice al petto. (Lo studente mette giù il braccio e alza un pollice.) Se ottieni più risposte, mostrami tenendo più dita. (Aspetta per 30 secondi Molti studenti stanno tenendo in mano più dita, anche se molti hanno solo un pollice: l'insegnante vede se qualcuno non ha risolto il problema: questa è una grande opportunità per la valutazione formativa.
Chiamare gli studenti per le loro risposte, a partire da quelli che hanno una sola soluzione.)
Insegnante: Lucy?
Lucy: 26. (L'insegnante scrive 26 sulla lavagna).
Insegnante: Charles?
Charles: 107 (l'insegnante scrive 107 alla lavagna).
Insegnante: Michelle?
Michelle: 25. (L'insegnante scrive 25 sulla lavagna).
Insegnante: altre risposte? (Nessuno ne ha). Chi vorrebbe spiegare come hanno ottenuto la loro risposta? Tyrone?
(L'insegnante registra ciò che gli studenti scrivono mentre spiegano).
Tyrone: So che 9 + 7 è 16, e poi ne ho aggiunti altri 10 per ottenere 26.
Sarah: 10 + 17 è 27, e 10 è 1 più di 9, quindi 9 + 17 deve essere 26.
Charles: 9 + 1 è 10, e poi metti un 7 dopo, quindi è 107.
Lucy: Ho contato uno per uno, ma mi sono appena accorto di aver sbagliato. Sono d'accordo con 26
(L'insegnante esce 25 e lo sostituisce con 26.)
Sam: Sono rispettosamente in disaccordo con Charles. Non puoi aggiungere il 9 + 1 perché il 1 sta per 10.
Charles: Ma è così che aggiungi. L'ho fatto bene
(L'insegnante lascia continuare la conversazione fino a quando il consenso della classe è raggiunto. Nel frattempo, annota i ragionamenti degli studenti sulle soluzioni con cui non sono d'accordo)

Strategie
Suggerimenti
Una volta annotate tutte le soluzioni, l'insegnante chiede agli studenti di spiegare come hanno ottenuto la loro soluzione. Gli studenti spiegano (dal loro posto) mentre l'insegnante scrive i passi che descrivono alla lavagna.
- Discussione e consenso. Idealmente, entro la fine della discussione, la classe dovrebbe avere una lista di 3-6 diversi approcci al problema, oltre a un consenso su quale sia la risposta corretta.
- Azione supplementare. L'insegnante ha quindi la possibilità di porre una domanda successiva che si basa sull'ultima. (Se 9 +17 fosse la prima domanda, 9 + 27 o 19 + 17 potrebbe essere la fase successiva).

Insegnante:
(Scrive 9 + 17 alla lavagna). (Uno studente inizia a muovere il braccio in aria.) Quando hai la risposta, mostrami il pollice al petto. (Lo studente mette giù il braccio e alza un pollice.) Se ottieni più risposte, mostrami tenendo più dita. (Aspetta per 30 secondi Molti studenti stanno tenendo in mano più dita, anche se molti hanno solo un pollice: l'insegnante vede se qualcuno non ha risolto il problema: questa è una grande opportunità per la valutazione formativa.
Chiamare gli studenti per le loro risposte, a partire da quelli che hanno una sola soluzione.)
Insegnante: Lucy?
Lucy: 26. (L'insegnante scrive 26 sulla lavagna).
Insegnante: Charles?
Charles: 107 (l'insegnante scrive 107 alla lavagna).
Insegnante: Michelle?
Michelle: 25. (L'insegnante scrive 25 sulla lavagna).
Insegnante: altre risposte? (Nessuno ne ha). Chi vorrebbe spiegare come hanno ottenuto la loro risposta? Tyrone?
(L'insegnante registra ciò che gli studenti scrivono mentre spiegano).
Tyrone: So che 9 + 7 è 16, e poi ne ho aggiunti altri 10 per ottenere 26.
Sarah: 10 + 17 è 27, e 10 è 1 più di 9, quindi 9 + 17 deve essere 26.
Charles: 9 + 1 è 10, e poi metti un 7 dopo, quindi è 107.
Lucy: Ho contato uno per uno, ma mi sono appena accorto di aver sbagliato. Sono d'accordo con 26
(L'insegnante esce 25 e lo sostituisce con 26.)
Sam: Sono rispettosamente in disaccordo con Charles. Non puoi aggiungere il 9 + 1 perché il 1 sta per 10.
Charles: Ma è così che aggiungi. L'ho fatto bene
(L'insegnante lascia continuare la conversazione fino a quando il consenso della classe è raggiunto. Nel frattempo, annota i ragionamenti degli studenti sulle soluzioni con cui non sono d'accordo)
Strategie
Le potenziali risposte che i tuoi studenti potrebbero fornire
Alcune potenziali strategie per l'addizione includono:
- counting all
- counting on
- doppio / vicino al doppio
- comporre decine
- numeri amici (es. 23 + 48 - Lo studente addiziona 48 + 2 per ottenere 23 +50 = 73 e poi toglie 2 da 71
- compensazione (ad esempio, 8 + 6 Lo studente prende uno da 8 e lo aggiunge a 6 per ottenere 7 + 7)
- scomposizione numerica secondo il valore posizionale (ad es. 12 + 43 diventa (10 + 40 e 2 + 3)
- addizione secondo il valore posizionale (ad esempio, 45 + 28 Lo studente inizia addizionando 45 + 20 = 65 e poi 65 +8 = 73)
Alcune potenziali strategie per la sottrazione includono:
- sommando
- scomposizioni in numeri facili da sottrarre, ad esempio, 65 - 32 Lo studente la pensa come 65 - (10 + 10 + 10 + 2)
- scomponendo e sottraendo secondo il valore posizionale
Suggerimenti
- Inizia con domande facili accessibili a tutti.
- Gli studenti cercheranno di vedere se indichi quale sia la risposta giusta. Non favorire le risposte giuste rispetto a quelle sbagliate. Assicurati che le spiegazioni siano ciò che conta.
- Prendersi qualche minuto per pianificare una sequenza di domande può essere utile. (cioè, inizierò con 9+7, poiché tutti possono farlo, quindi faremo 9+17, poi 19+17.)
- Assicurati di enfatizzare il protocollo di conversazione numerica con le mani al petto piuttosto che agitarle in aria.
- Dai agli studenti un linguaggio costruttivo da usare nella discussione, come "Io rispettosamente non sono d'accordo, perché ..." e "Sono d'accordo con _____, perché ..."
- Mantenere sempre l'ambiente sicuro e positivo.
- Non preoccuparti se non raggiungi un consenso totale su ogni problema. A volte uno studente avrà bisogno di più tempo per elaborare. Puoi andare avanti quando sembra che sia il momento.
- Le conversazioni numeriche possono espandersi se non stai attento. Fare discorsi numerici brevi (5 minuti) è più efficace di quelli lunghi di rado.
- Number Talks consente agli studenti di pensare in modo flessibile con i numeri, dando loro la possibilità di scomporre i numeri e rendere i problemi più facili.
ATTIVITA'
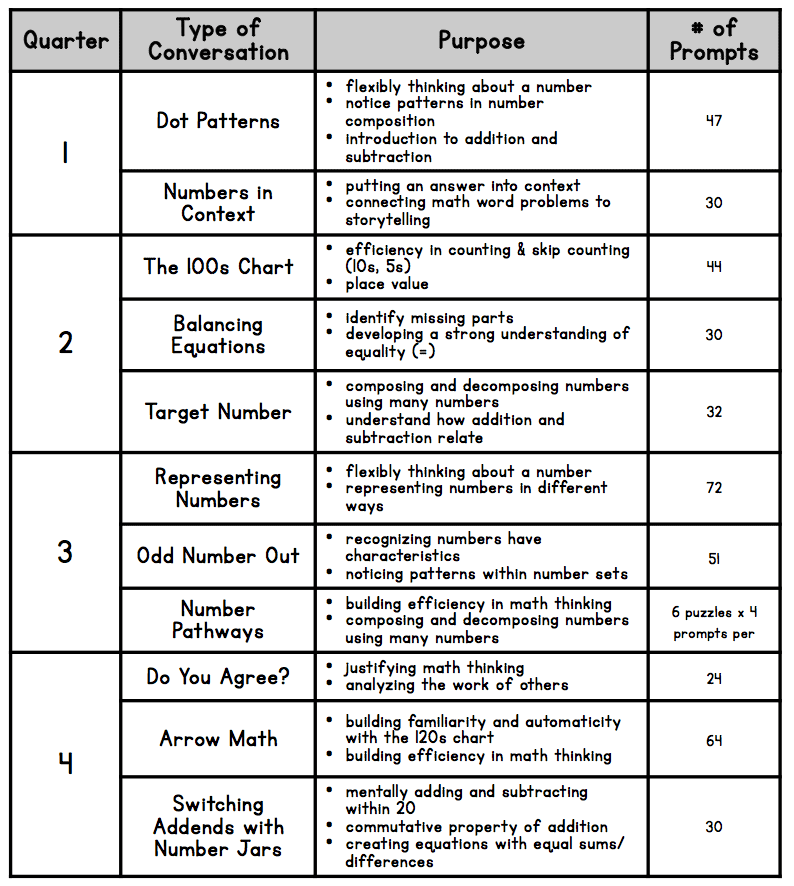
Gli studenti devono capire che 7 può essere fatto da 4 e 3, 2 e 5, 6 e 1, o 7 e 0.
Agli studenti viene fornito un "Numero obiettivo" e chiesto di usare alcuni dei numeri forniti per raggiungere l'obiettivo. Gli studenti devono quindi decidere quanti numeri utilizzare, quale operazione usare (addizione o sottrazione) e poi decidere se l'ordine numerico è importante.
 Una parte importante dell'insegnamento agli studenti è la fluidità e la flessibilità numerica .
Una parte importante dell'insegnamento agli studenti è la fluidità e la flessibilità numerica .
Essi dovrebbero essere in grado di incontrare numeri secondo una varietà di formati e interagire con loro in vari modi. Durante le conversazioni sulle rappresentazioni dei numeri , incoraggiare gli studenti a escludere il tipico frame di dieci, più uno, ecc. Queste sono ottime strategie quando iniziamo, ma dopo i primi giorni gli studenti possono costruire queste rappresentazioni di base per sviluppare relazioni e comprensione.

MATERIALI
Ideas for Number Talks
NumberTalks Article S.Parrish
Quick Image 100 ten frames











Nessun commento:
Posta un commento